The almost universal position among financial planners, and those in the financial media is that investors with an eye on retirement should reduce the “risk” of their portfolio with age. This is typically expressed with simple heuristics such as “let the equity share of a retirement plan be 110 minus the age of the investor.” This creates a natural Glidepath, meaning that the equity share of the portfolio glides downward in a gentle way over time. Such simple rules are comforting, easy to implement, and intuitively appealing. The argument most often used for this strategy is that as one ages, one has fewer years to recover when stock markets drop. Thus, it becomes much safer to move away from equities with age.
Unfortunately, the data suggests that this is a pretty bad idea for multiple reasons. Bonds don’t change their payouts due to inflation. When inflation rises, the bond payout does not, and this kills the real value of the bonds. Equities can also fall with inflation, but they will eventually increase in value later. For example, the US Treasury bonds lost 17.8% in 2022 while the S&P 500 index lost 18%. On the other hand, the same bond funds yielded roughly 6% in 2023 (as of this writing) while the S&P 500 yielded 23%. The higher average returns on equities makes the falls recoverable to a much greater extent than it does with bonds
You can also think of this another way. If I look up tomorrow and Ford trucks are selling at $1,000,000 each due to inflation, eventually the price of Ford stock is going to reflect that. In other words, inflation in prices of goods has to eventually lead to inflation in the prices of the companies that make those goods. At the same time, inflation won’t increase the price of your bonds because their payoffs don’t change with inflation. Consequently, the bond must fall in price to deliver the same return.
However, if we move away from the “time to recover” argument, there is still a coherent rationale for moving to bonds with age. Much of the theoretical underpinning of this idea can be traced to a paper from Paul Samuelson in 1975 (Samuelson 1975). In that work, Prof Samuelson stated that you can think of your total portfolio as having 2 large pieces but he didn’t mean stocks and bonds. He was referring to your Human Capital (HC) and your Financial Capital (FC). The human capital is essentially the present value of your future earnings. This capital will be paid out over time like a bond. If one is a tenured Professor at Stanford as Prof Samuelson was when he wrote this paper, this cash flow is virtually risk-free, so Prof Samuelson was holding the equivalent of a very large bond in his virtual portfolio. As a result, he was able to accommodate having a large share of his FC in the form of equities. This FC is all financial holdings including real estate, retirement accounts, brokerage accounts, etc. As one ages, the number of remaining working years shrinks, thus the HC also shrinks. In order to keep the same balance between risky and risk-free assets, it is necessary to reduce the level of risky assets. Thus, we would cut back on equities in this portfolio over time.
This makes almost all risk-averse people feel better, which is virtually all humans. That’s why every financial writer repeats it endlessly. However, I never really bought the argument for 3 reasons (really 4). First, when I look at Prof Samuelson’s paper the central idea is conveyed in this equation:
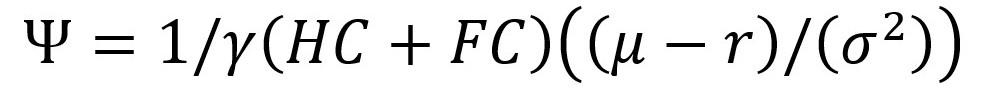
The left hand side of the equation shows the optimal portion of the portfolio that is “risky”. Simply put, imagine a portfolio with a risk-free asset and a risky one. Ψ is the money in the risky asset. HC is human capital that is shrinking over time, but will be treated as risk free. FC is the financial capital that is probably growing over time and is certainly risky. γ reflects the level of risk aversion and ranges from 1 to 5, but for me its about 1 or 2. r is the risk-free rate of return (let’s say around 2%), µ is the average return on equities (let’s say around 8%). As an illustration, if HC = FC = $500,000, the optimal level of stocks in this portfolio is,
Ψ= ½ ($500,000 + $500,000)((.08 – 0.02)/(0.22) = $500,000 (0.06/0.04) = $500,000 * 3/2
This turns out to be $750,000. But wait, I thought you said I only have $500,000 in financial capital in total. Therein lies the problem. Since 750 > 500 the best you can do is to keep 100% of your FC in stocks.
Even if you are 60 years old (like me), if you have income exceeding $100,000 per year and $1,000,000 in a retirement account, the optimal allocation to stocks is easily over $1,000,000. In other words, the optimal allocation to stocks is more than all the financial assets in hand, so there is really no decision to make here.
But wait, there’s more. Let’s say that FC is $1,000,000 and the only HC you count is your future Social Security (SSI) checks. I am willing to think of this as risk-free, or at least as risk-free as any other treasury bond. If your remaining life expectancy is over 10 years, this value can easily exceed $300,000. In this case the optimal amount in stocks turns out to be $975,000. It’s like saying that as you age, your optimal amount of money invested in stocks drops from 200% of when you are young, to 100% a decade or two later, and virtually 100% at retirement. Technically, that is a reduction over time, but as a practical matter all you did was move from “all that you have to invest” to “all that you have to invest.” No meaningful difference. Some researchers have argued that this really means you should borrow money to buy stocks when you are young (See Ayres and Nalebuff 2013 for discussion,.) However, I am not willing to go that far, and most banks are not willing to lend you much money to do so anyway, because your FC is the only collateral that they care about.
The second reason I don’t like this strategy is that it doesn’t appear to work very well. For example, a recent paper by Javier Estrada (Estrada2014) in the Journal of Portfolio Management looked at historical data from 19 countries over 110 years to consider simple Glidepath strategies. The Glidepath approach is implemented in most retirement accounts under the name of Target Date Funds. Again, in this approach the bond allocation is increased each year. In fact, this is the default account selection in most retirement plans. As a result, if you have never looked at this closely, this is probably what you have. Estrada, compared returns from a simple Glidepath strategy to a “Balanced” strategy where the equity portion was held constant, and a “Contrarian” strategy where you do the exact opposite. In other words, you increase the equity share of the portfolio over time. He found that the Balanced strategy fared better than the Glidepath strategy, and the Contrarian strategy performed best of all even though the variance of returns is higher. As he explains,
“…the higher uncertainty of contrarian strategies is basically uncertainty about how much better, not how much worse investors are expected to fare”
In short, the contrarian strategy produced a greater average ending value, and did so with lower downside risk. I’ll take that every time.
Third, evidence strongly suggest that most people become less risk-averse as they become more wealthy. Prof Samuelson has stated that this observation applies to him. In a more recent paper, Prof Francisco Gomes (Gomes21) argued that the generally accepted claim that the share of a retirement account dedicated to stocks should always shrink with age, is incomplete for this very reason. Technically, speaking he found evidence of “Decreasing Marginal Risk Aversion” meaning that as the level of wealth rises, people are willing to take on more risk. Much of this is based on the observation that the willingness to hold a larger portion of assets in stocks increases with the level of wealth. The nice thing about thinking about risk aversion, is that if you tolerate more risk, that pretty much convinces me that your level of risk aversion has fallen. I don’t really need a fancy argument here. If those with more wealth tolerate more risk, that kind of says that having more wealth increases risk tolerance.
The fourth, and by far the most significant reason I do not fall into the Glidepath camp is that my planning horizon never seems to shrink, and I am willing to bet that yours won’t either. When I was about 8 years old, my father came to me with a set of paint swatches on cards and asked me to pick a color to paint the house. Being 8 years old, I picked the brightest yellow that was presented. My father then went to the store and bought 5 gallons of bright yellow paint, and became the laughing stock of the neighborhood for the next 10 years. My appalled mother asked, why a grown man would give such a decision to a child, and my father explained. “It’s not really our house. It’s his house. We are just holding it for him until we die.” His planning horizon was never his lifetime – it was the lifespans of his children and grandchildren.
Ask yourself this question – which would you prefer: an easy retirement and poor grandchildren or a difficult retirement and rich grandchildren? I will make my portfolio more conservative as soon as my planning horizon shortens, but as long as I believe that my children will re-produce, that’s simply never going to happen.